本文共 6978 字,大约阅读时间需要 23 分钟。
最近这段时间系统性的学习了 BP 算法后写下了这篇学习笔记,因为能力有限,若有明显错误,还请指正。
什么是梯度下降和链式求导法则
假设我们有一个函数 J(w),如下图所示。
梯度下降示意图
现在,我们要求当 w 等于什么的时候,J(w) 能够取到最小值。从图中我们知道最小值在初始位置的左边,也就意味着如果想要使 J(w) 最小,w的值需要减小。而初始位置的切线的斜率a > 0(也即该位置对应的导数大于0),w = w – a 就能够让 w 的值减小,循环求导更新w直到 J(w) 取得最小值。如果函数J(w)包含多个变量,那么就要分别对不同变量求偏导来更新不同变量的值。
所谓的链式求导法则,就是求复合函数的导数:
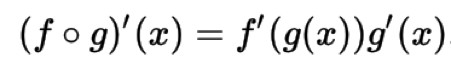
链式求导法则
放个例题,会更加明白一点:

链式求导的例子
神经网络的结构
神经网络由三部分组成,分别是最左边的输入层,隐藏层(实际应用中远远不止一层)和最右边的输出层。层与层之间用线连接在一起,每条连接线都有一个对应的权重值 w,除了输入层,一般来说每个神经元还有对应的偏置 b。
除了输入层的神经元,每个神经元都会有加权求和得到的输入值 z 和将 z 通过 Sigmoid 函数(也即是激活函数)非线性转化后的输出值 a,他们之间的计算公式如下
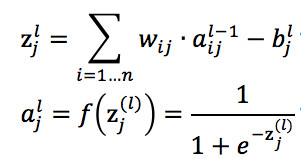
神经元输出值 a 的计算公式
其中,公式里面的变量l和j表示的是第 l 层的第 j 个神经元,ij 则表示从第 i 个神经元到第 j 个神经元之间的连线,w 表示的是权重,b 表示的是偏置,后面这些符号的含义大体上与这里描述的相似,所以不会再说明。下面的 Gif 动图可以更加清楚每个神经元输入输出值的计算方式(注意,这里的动图并没有加上偏置,但使用中都会加上)
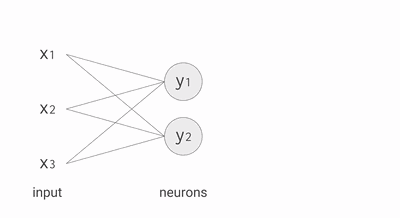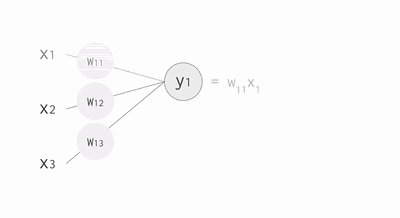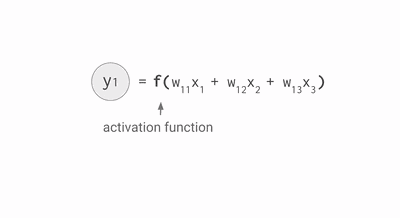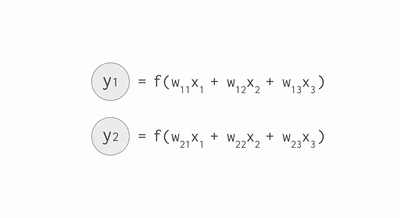
动图显示计算神经元输出值
使用激活函数的原因是因为线性模型(无法处理线性不可分的情况)的表达能力不够,所以这里通常需要加入 Sigmoid 函数来加入非线性因素得到神经元的输出值。
可以看到 Sigmoid 函数的值域为 (0,1) ,若对于多分类任务,输出层的每个神经元可以表示是该分类的概率。当然还存在其他的激活函数,他们的用途和优缺点也都各异。
BP 算法执行的流程(前向传递和逆向更新)
在手工设定了神经网络的层数,每层的神经元的个数,学习率 η(下面会提到)后,BP 算法会先随机初始化每条连接线权重和偏置,然后对于训练集中的每个输入 x 和输出 y,BP 算法都会先执行前向传输得到预测值,然后根据真实值与预测值之间的误差执行逆向反馈更新神经网络中每条连接线的权重和每层的偏好。在没有到达停止条件的情况下重复上述过程。
其中,停止条件可以是下面这三条
● 权重的更新低于某个阈值的时候
● 预测的错误率低于某个阈值
● 达到预设一定的迭代次数
譬如说,手写数字识别中,一张手写数字1的图片储存了28*28 = 784个像素点,每个像素点储存着灰度值(值域为[0,255]),那么就意味着有784个神经元作为输入层,而输出层有10个神经元代表数字0~9,每个神经元取值为0~1,代表着这张图片是这个数字的概率。
每输入一张图片(也就是实例),神经网络会执行前向传输一层一层的计算到输出层神经元的值,根据哪个输出神经元的值最大来预测输入图片所代表的手写数字。
然后根据输出神经元的值,计算出预测值与真实值之间的误差,再逆向反馈更新神经网络中每条连接线的权重和每个神经元的偏好。
前向传输(Feed-Forward)
从输入层=>隐藏层=>输出层,一层一层的计算所有神经元输出值的过程。
逆向反馈(Back Propagation)
因为输出层的值与真实的值会存在误差,我们可以用均方误差来衡量预测值和真实值之间的误差。
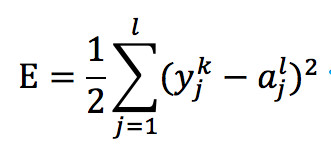
均方误差
逆向反馈的目标就是让E函数的值尽可能的小,而每个神经元的输出值是由该点的连接线对应的权重值和该层对应的偏好所决定的,因此,要让误差函数达到最小,我们就要调整w和b值, 使得误差函数的值最小。
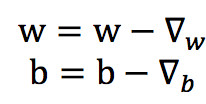
权重和偏置的更新公式
对目标函数 E 求 w 和 b 的偏导可以得到 w 和 b 的更新量,下面拿求 w 偏导来做推导。
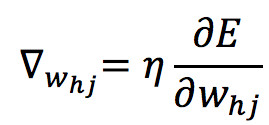
其中 η 为学习率,取值通常为 0.1 ~ 0.3,可以理解为每次梯度所迈的步伐。注意到 w_hj 的值先影响到第 j 个输出层神经元的输入值a,再影响到输出值y,根据链式求导法则有:
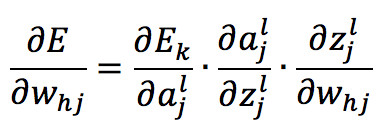
使用链式法则展开对权重求偏导
根据神经元输出值 a 的定义有:
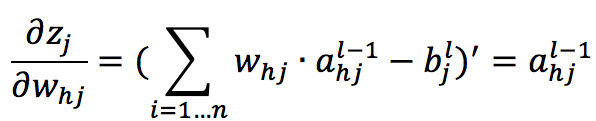
对函数 z 求 w 的偏导
Sigmoid 求导数的式子如下,从式子中可以发现其在计算机中实现也是非常的方便:
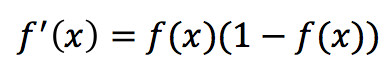
Sigmoid 函数求导
所以
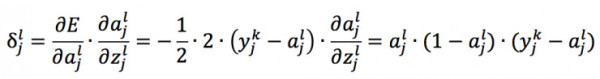
则权重 w 的更新量为:
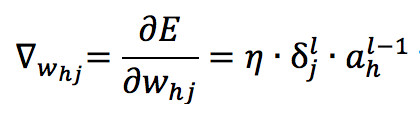
类似可得 b 的更新量为:
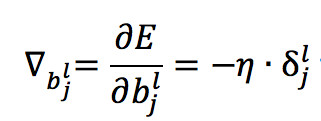
但这两个公式只能够更新输出层与前一层连接线的权重和输出层的偏置,原因是因为 δ 值依赖了真实值y这个变量,但是我们只知道输出层的真实值而不知道每层隐藏层的真实值,导致无法计算每层隐藏层的 δ 值,所以我们希望能够利用 l+1 层的 δ 值来计算 l 层的 δ 值,而恰恰通过一些列数学转换后可以做到,这也就是逆向反馈名字的由来,公式如下:
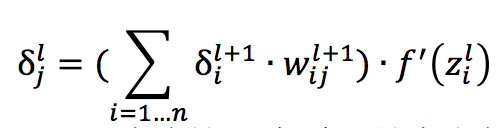
从式子中我们可以看到,我们只需要知道下一层的权重和神经元输出层的值就可以计算出上一层的 δ 值,我们只要通过不断的利用上面这个式子就可以更新隐藏层的全部权重和偏置了。
在推导之前请先观察下面这张图:
首先我们看到 l 层的第 i 个神经元与 l+1 层的所有神经元都有连接,那么我们可以将 δ 展开成如下的式子:
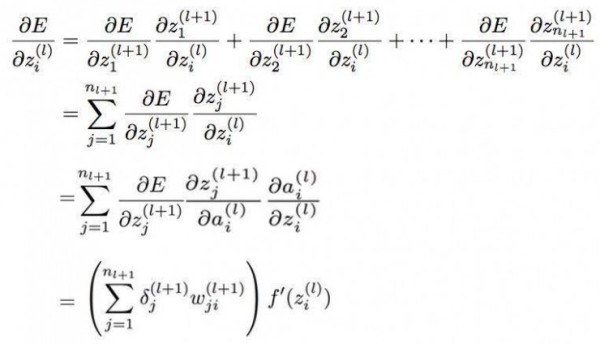
也即是说我们可以将 E 看做是 l+1 层所有神经元输入值的 z 函数,而上面式子的 n 表示的是 l+1 层神经元的数量,再进行化简后就可以得到上面所说的式子。
在这里的推导过程只解释了关键的部分。另外也参考了周志华所写的机器学习中的神经网络部分的内容和 neural networks and deep learning的内容。
Python 源码解析
源码来自于 Michael Nielsen大神的深度学习在线教程。
使用 Python 实现的神经网络的代码行数并不多,仅包含一个 Network 类,首先来看看该类的构造方法。
- def __init__(self, sizes):
- """
- :param sizes: list类型,储存每层神经网络的神经元数目
- 譬如说:sizes = [2, 3, 2] 表示输入层有两个神经元、
- 隐藏层有3个神经元以及输出层有2个神经元
- """
- # 有几层神经网络
- self.num_layers = len(sizes)
- self.sizes = sizes
- # 除去输入层,随机产生每层中 y 个神经元的 biase 值(0 - 1)
- self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
- # 随机产生每条连接线的 weight 值(0 - 1)
- self.weights = [np.random.randn(y, x)
- for x, y in zip(sizes[:-1], sizes[1:])]
向前传输(FreedForward)的代码
- def feedforward(self, a):
- """
- 前向传输计算每个神经元的值
- :param a: 输入值
- :return: 计算后每个神经元的值
- """
- for b, w in zip(self.biases, self.weights):
- # 加权求和以及加上 biase
- a = sigmoid(np.dot(w, a)+b)
- return a
源码里使用的是随机梯度下降(Stochastic Gradient Descent,简称 SGD),原理与梯度下降相似,不同的是随机梯度下降算法每次迭代只取数据集中一部分的样本来更新 w 和 b 的值,速度比梯度下降快,但是,它不一定会收敛到局部极小值,可能会在局部极小值附近徘徊。
- def SGD(self, training_data, epochs, mini_batch_size, eta,
- test_data=None):
- """
- 随机梯度下降
- :param training_data: 输入的训练集
- :param epochs: 迭代次数
- :param mini_batch_size: 小样本数量
- :param eta: 学习率
- :param test_data: 测试数据集
- """
- if test_data: n_test = len(test_data)
- n = len(training_data)
- for j in xrange(epochs):
- # 搅乱训练集,让其排序顺序发生变化
- random.shuffle(training_data)
- # 按照小样本数量划分训练集
- mini_batches = [
- training_data[k:k+mini_batch_size]
- for k in xrange(0, n, mini_batch_size)]
- for mini_batch in mini_batches:
- # 根据每个小样本来更新 w 和 b,代码在下一段
- self.update_mini_batch(mini_batch, eta)
- # 输出测试每轮结束后,神经网络的准确度
- if test_data:
- print "Epoch {0}: {1} / {2}".format(
- j, self.evaluate(test_data), n_test)
- else:
- print "Epoch {0} complete".format(j)
根据 backprop 方法得到的偏导数更新 w 和 b 的值。
- def update_mini_batch(self, mini_batch, eta):
- """
- 更新 w 和 b 的值
- :param mini_batch: 一部分的样本
- :param eta: 学习率
- """
- # 根据 biases 和 weights 的行列数创建对应的全部元素值为 0 的空矩阵
- nabla_b = [np.zeros(b.shape) for b in self.biases]
- nabla_w = [np.zeros(w.shape) for w in self.weights]
- for x, y in mini_batch:
- # 根据样本中的每一个输入 x 的其输出 y,计算 w 和 b 的偏导数
- delta_nabla_b, delta_nabla_w = self.backprop(x, y)
- # 累加储存偏导值 delta_nabla_b 和 delta_nabla_w
- nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
- nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
- # 更新根据累加的偏导值更新 w 和 b,这里因为用了小样本,
- # 所以 eta 要除于小样本的长度
- self.weights = [w-(eta/len(mini_batch))*nw
- for w, nw in zip(self.weights, nabla_w)]
- self.biases = [b-(eta/len(mini_batch))*nb
- for b, nb in zip(self.biases, nabla_b)]
下面这块代码是源码最核心的部分,也即 BP 算法的实现,包含了前向传输和逆向反馈,前向传输在 Network 里有单独一个方法(上面提到的 feedforward 方法),那个方法是用于验证训练好的神经网络的精确度的,在下面有提到该方法。
- def backprop(self, x, y):
- """
- :param x:
- :param y:
- :return:
- """
- nabla_b = [np.zeros(b.shape) for b in self.biases]
- nabla_w = [np.zeros(w.shape) for w in self.weights]
- # 前向传输
- activation = x
- # 储存每层的神经元的值的矩阵,下面循环会 append 每层的神经元的值
- activations = [x]
- # 储存每个未经过 sigmoid 计算的神经元的值
- zs = []
- for b, w in zip(self.biases, self.weights):
- z = np.dot(w, activation)+b
- zs.append(z)
- activation = sigmoid(z)
- activations.append(activation)
- # 求 δ 的值
- delta = self.cost_derivative(activations[-1], y) * \
- sigmoid_prime(zs[-1])
- nabla_b[-1] = delta
- # 乘于前一层的输出值
- nabla_w[-1] = np.dot(delta, activations[-2].transpose())
- for l in xrange(2, self.num_layers):
- # 从倒数第 **l** 层开始更新,**-l** 是 python 中特有的语法表示从倒数第 l 层开始计算
- # 下面这里利用 **l+1** 层的 δ 值来计算 **l** 的 δ 值
- z = zs[-l]
- sp = sigmoid_prime(z)
- delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
- nabla_b[-l] = delta
- nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
- return (nabla_b, nabla_w)
接下来则是 evaluate 的实现,调用 feedforward 方法计算训练好的神经网络的输出层神经元值(也即预测值),然后比对正确值和预测值得到精确率。
- def evaluate(self, test_data):
- # 获得预测结果
- test_results = [(np.argmax(self.feedforward(x)), y)
- for (x, y) in test_data]
- # 返回正确识别的个数
- return sum(int(x == y) for (x, y) in test_results)
最后,我们可以利用这个源码来训练一个手写数字识别的神经网络,并输出评估的结果,代码如下:
- import mnist_loader
- import network
- training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
- net = network.Network([784, 30, 10])
- net.SGD(training_data, 30, 10, 3.0, test_data = test_data)
- # 输出结果
- # Epoch 0: 9038 / 10000
- # Epoch 1: 9178 / 10000
- # Epoch 2: 9231 / 10000
- # ...
- # Epoch 27: 9483 / 10000
- # Epoch 28: 9485 / 10000
- # Epoch 29: 9477 / 10000
可以看到,在经过 30 轮的迭代后,识别手写神经网络的精确度在 95% 左右,当然,设置不同的迭代次数,学习率以取样数对精度都会有影响,如何调参也是一门技术活,这个坑就后期再填吧。
总结
神经网络的优点:
网络实质上实现了一个从输入到输出的映射功能,而数学理论已证明它具有实现任何复杂非线性映射的功能。这使得它特别适合于求解内部机制复杂的问题。
网络能通过学习带正确答案的实例集自动提取“合理的”求解规则,即具有自学习能力。
网络具有一定的推广、概括能力。
神经网络的缺点:
对初始权重非常敏感,极易收敛于局部极小。
容易 Over Fitting 和 Over Training。
如何选择隐藏层数和神经元个数没有一个科学的指导流程,有时候感觉就是靠猜。
应用领域:
常见的有图像分类,自动驾驶,自然语言处理等。
TODO
但其实想要训练好一个神经网络还面临着很多的坑(譬如下面四条):
- 如何选择超参数的值,譬如说神经网络的层数和每层的神经元数量以及学习率;
- 既然对初始化权重敏感,那该如何避免和修正;
- Sigmoid 激活函数在深度神经网络中会面临梯度消失问题该如何解决;
- 避免 Overfitting 的 L1 和 L2正则化是什么。
转载地址:http://anwva.baihongyu.com/